Models and Transformations
Table of Contents
Accordingly, all of cognition is cognition in models or by means of models, and in general, any human encounter with the world needs "model" as the mediator […]. — Herbert Stachowiak (Podnieks 2017)
At the core of Model-Driven Engineering (MDE) sit two key concepts: that of models and of transformations. These notions are so central to MDE that Brambilia et al. distilled the entire discipline into the following equation (Brambilla, Cabot, and Wimmer 2012) (p. 8):
\begin{align} Models + Transformations &= Software \end{align}This document provides an overview of both of these concepts. It is organised as follows. It starts by determining the need for models in the first instance (Section Why Model?), and then elaborates more precisely what is meant by the term model in this context (Section What Kind of Model?). Next, we analyse the relationship between models and metamodels (Section Models and Metamodels) as well as their hierarchical nature (Section Metamodelling Hierarchy). Following this, we provide a context for modeling languages, first by looking at their purpose (Section Modeling Languages and Their Purposes) and then by contrasting and comparing them with the better known programming languages (Section Modeling Languages and Programming Languages).
Let us begin then by considering the role of models in the general case.
Why Model?
Unlike the difficulties faced in defining MDE's boundaries (cf. Conditions at the Boundaries), the literature presents a far more consensual picture on the reasons for modeling. Predictably, it emanates mainly from without, given the importance of models in most scientific and engineering contexts. Due to this, we have limited our excursion to two often cited sources in the early MDE literature: Rothenberg and Stachowiak.
In "General Model Theory" (Stachowiak 1973), Stachowiak proposes a model-based concept of cognition and identifies three principal features of models:
- Mapping: Models map individuals, original or artificial, to a category of all such individuals sharing similar properties. The object of the mapping could itself be a model, thus allowing for complex composition.
- Reduction: Models focus only on a subset of the individual's properties, ignoring aspects that are deemed irrelevant.
- Pragmatism: Models have a purpose as defined by its creators, which guides the modeling process. Stachowiak states (emphasis ours): "[models] are not only models of something. They are also models for somebody, a human or an artificial model user. They perform therefore their functions in time, within a time interval. And they are finally models for a definite purpose."1
Much of the expressive power of models arises from these three fundamental properties.
For his part, Rothenberg's contribution (Rothenberg et al. 1989) also gives a deep insight into the nature of models and the modeling process2 and, in particular, his statements on substitutability are of keen interest when uncovering the reasons for modeling (emphasis his):
Modeling, in the broadest sense, is the cost-effective use of something in place of something else for some cognitive purpose. It allows us to use something that is simpler, safer or cheaper than reality instead of reality for some purpose. A model represents reality for the given purpose; the model is an abstraction of reality in the sense that it cannot represent all aspects of reality. This allows us to deal with the world in a simplified manner, avoiding the complexity, danger and irreversibility of reality.
Taken together, the properties identified by Rothenberg and Stachowiak make it clear that software engineering is inevitably deeply connected to models and modeling, as is any other human endeavour that involves cognition. However, this implicit understanding only scratches the surface of possibilities. In order to extract all of the potential of the modeling activity, explicit introspection is necessary. Evans eloquently explains why it must be so (emphasis ours):
To create software that is valuably involved in users' activities, a development team must bring to bear a body of knowledge related to those activities. The breadth of knowledge required can be daunting. The volume and complexity of information can be overwhelming. Models are tools for grappling with this overhead. A model is a selectively simplified and consciously structured form of knowledge. An appropriate model makes sense of information and focuses it on a problem. (Evans 2004) (p. 3)
Therefore, it is important to model consciously; with a purpose. In order to do so, one must first start with a better understanding of what is meant by "model" in the context of the target domain.
What Kind of Model?
The term model is used informally by software engineers as a shorthand for any kind of abstract representation of a system's function, behaviour or structure.3 Ever critical in matters of rigour, Jörges et al. (Jörges 2013) (p. 13) remind us that "[the] existence of MD* approaches and numerous corresponding tools […] indicates that there seems to be at least a common intuition of what a model actually is. However, there is still no generally accepted definition of the term 'model'." In typical pragmatic form, Bézivin (Bézivin 2005a) provides what he calls an "operational engineering definition of a 'model'" (emphasis ours): "[…] a graph-based structure representing some aspects of a given system and conforming to the definition of another graph called a metamodel." Stahl et al. call this a formal model (NO_ITEM_DATA:Stahl:2006:MSD:1196766) (p. 58).
The crux here is to address ambiguity. A formal model is one which is expressed using a formal language, called the modeling language, and designed specifically for the purpose of modeling well-defined aspects of a problem domain. A modeling language needs to be a formal language because it must have well-defined syntax and semantics, required in order to determine if its instances are well-formed or not. The next sections provide an overview of these two topics; since the literature was found to be largely consensual, the focus is solely on their exposition. We then join these two notions as we revisit the concept of metamodel.
Syntax
Syntax concerns itself with form, defining the basic building blocks of the language and the set of rules that determine their valid combinations. This is done in two distinct dimensions:
- Concrete Syntax: Specifies a physical representation of the language, textually or graphically. It can be thought of its external representation or notation, of which there can be one or more.
- Abstract Syntax: Specifies the language's underlying structure, independent of its concrete syntax. It can be thought of as its internal representation.
Semantics
Validation is not complete at the syntactic level, however, because a statement's validity may be dependent on context and therefore requiring an understanding of its semantics. Semantics deals with meaning and, as with syntax, it is also split across two distinct dimensions:
- Static Semantics: Concerns itself with contextual aspects that can be inferred from the abstract syntax representation of the model. In the case of a typed general purpose programming language, static semantics are comprised of a set of rules that determine if an expression is well-formed given the types involved. For modeling languages, the exact role of static semantics varies but is commonly concerned with placing constraints on types.
- Dynamic Semantics: These are only relevant to modeling languages whose instances can be executed and are thus also known as execution semantics. They define the execution behaviour of the various language constructs.
Models and Metamodels
Given these concepts, we can now elaborate further on Bezivin's definition above, and connect them from a modeling point of view. Formal models are instances of a modeling language, which provides the modeler with the vocabulary to describe entities from a domain. Together, the abstract syntax and the static semantics of the modeling language make up its metamodel, and instance models — by definition — must conform to it.
Employing terminology from Kottemann and Konsynsk (Kottemann and Konsynski 1984), the metamodel can be said to capture the deep structure that connects all of its instance models, and the instance models are expressed in the abstract syntax of the modeling language — its surface structure. Within this construct, we now have a very clear separation between the entities being modeled, the model and the model's metamodel as they exist at different layers of abstraction.4 However, the layering process does not end at the metamodel.
Metamodelling Hierarchy
Since all formal models are instances of a metamodel, the metamodel itself is no exception: it too must conform to a metametamodel. The metametamodel provides a generalised way to talk about metamodels and exists at a layer above that of the metamodel. Though in theory infinite, the layering process is typically curtailed at the metametamodel layer, since it is possible to create a metametamodel that conforms to itself.5,6
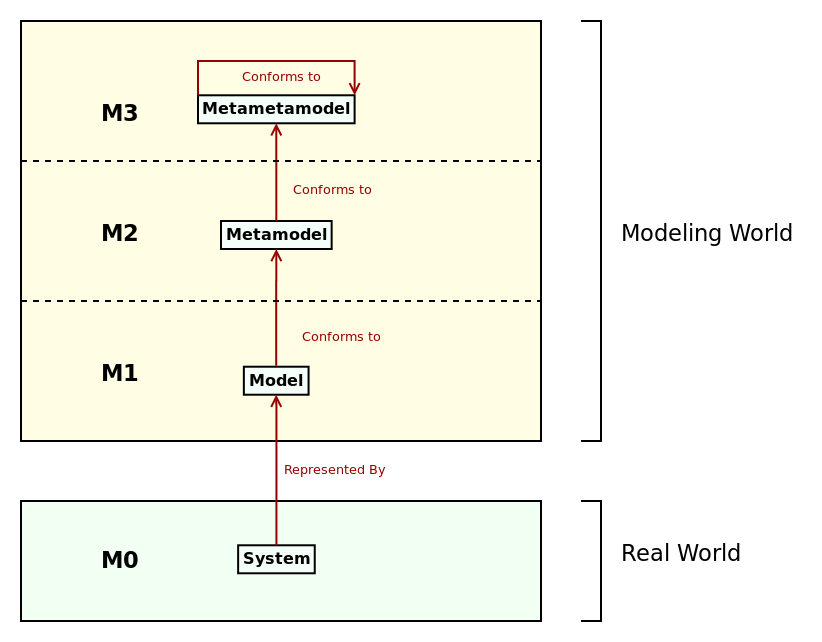
Figure 1: OMG four-layer metamodel architecture. Source: Author's drawing based on a diagram by Bézivin (Bézivin 2004).
Following on from the above-mentioned work of Kottemann and Konsynski (Kottemann and Konsynski 1984), and that of many others, the OMG standardised these notions of an abstraction hierarchy into a four-layer metamodel architecture that describes higher-order modeling. Bézivin (Bézivin 2005b) referred to it as the 3+1 architecture, and summarised it as follows: "[at] the bottom level, the M0 layer is the real system. A model represents this system at level M1. This model conforms to its metamodel defined at level M2 and the metamodel itself conforms to the metametamodel at level M3." Figure 1 illustrates the idea. Its worthwhile pointing out that the four-layer architecture is a typical example of the constant cross-pollination within MDE, as it was originally created in the context of what eventually became the MDA but nowadays is seen as part of the core MDE cannon itself (Brambilla, Cabot, and Wimmer 2012).7
As the literature traditionally explains the four layer model by means of an
example (Bézivin 2005b) (Brambilla, Cabot, and Wimmer 2012)
(Henderson-Sellers and Bulthuis 2012), we shall use a trivial model of cars to do so. It
is illustrated in Figure 2. Here, at M0, we have two cars
with licence plates "123-ABC" and "456-DEG". At M1, the two cars are abstracted
to the class Car, with a single attribute of type String: LicencePlate. At
M2, these concepts are further abstracted to the notions of a Class and
Attribute. Car is an instance of a Class, and its property LicencePlate
is an instance of Attribute. Finally, at M3, we introduce Class; M2's
Class and Attribute are both instances of M3's Class, as is M3's Class
itself.
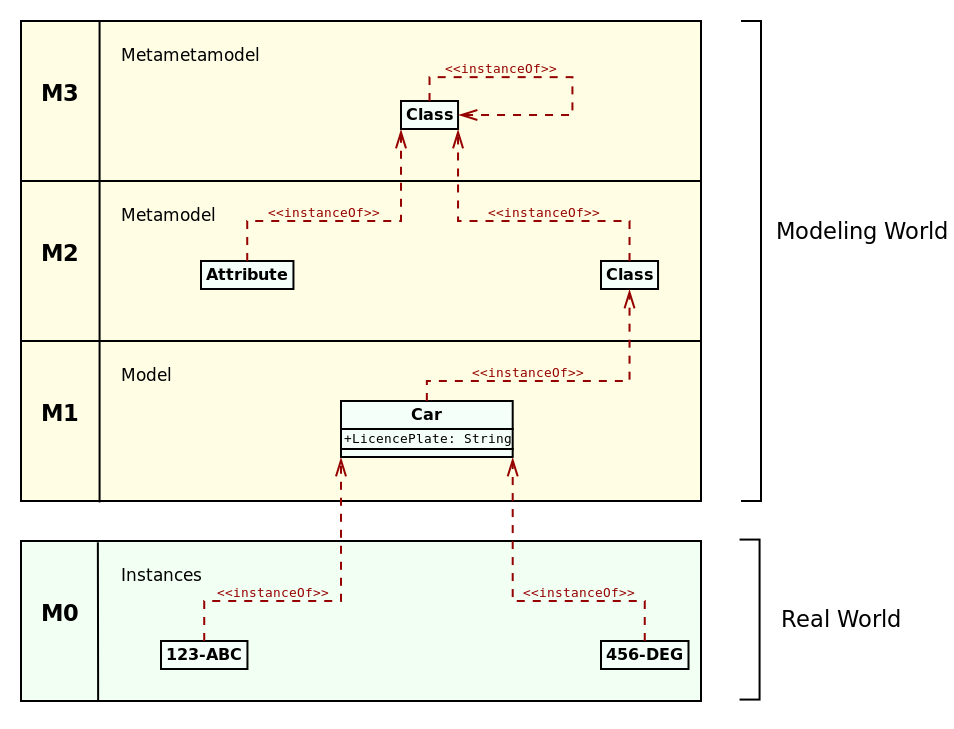
Figure 2: Example of the four-layer metamodel architecture. Source: Author's drawing based on a diagram by Brambilla et al. (Brambilla, Cabot, and Wimmer 2012) (p. 16)
The four-layer metamodel architecture has important properties. For example, whilst terms "model" and "meta" are often used in a relative (and even subjective) manner, within the architecture they now become concise — i.e., metametamodel is an unambiguous term within this framework. In addition, it was designed as a strict metamodeling framework. Atkinson and Kühne explain concisely the intent (emphasis theirs):
Strict metamodeling is based on the tenet that if a model A is an instance of another model B then every element of A is an instance-of some element in B. In other words, it interprets the instance-of relationship at the granularity of individual model elements. The doctrine of strict metamodeling thus holds that the instance-of relationship, and only the instance-of relationship, crosses meta-level boundaries, and that every instance-of relationship must cross exactly one meta-level boundary to an immediately adjacent level. (Atkinson and Kühne 2002)
Strict metamodeling is not the only possible approach — Atkinson and Kühne go on to describe loose metamodeling on the same paper — nor is the four-layer metamodel hierarchy itself free of criticism. On this regard, we'd like to single out the thorough work done by Henderson-Sellers et al. (Henderson-Sellers et al. 2013), who scoured the literature to identify the main problems with the architecture, and surveyed proposed "fixes", which ranged from small evolutionary changes to "paradigm shifting" modifications. Their work notwithstanding, our opinion is that, though the four-layer metamodel has limitations, it forms a reasonably well-understood abstraction which suffices for the purposes of our own research.
An additional point of interest — and one that perhaps may not be immediately obvious from the above diagrams — is that MDE encourages the creation of "multiple metamodels", each designed for a specific purpose, though ideally all conforming to the same metametamodel. As a result of this metamodel diversity — as well as due to other scenarios described on the next section — operations performed on models have become key to the modeling approach.
Models and Their Transformations
The second most significant component of MDE , after models, are Model Transformations (MTs) or just transforms. MTs are functions defined over metamodels and applied to their instance models. MTs receive one or more arguments, called the source models, and typically produce one or more models, called the target models. Source and target models must be formal models, and they may all conform to the same or to different metamodels.
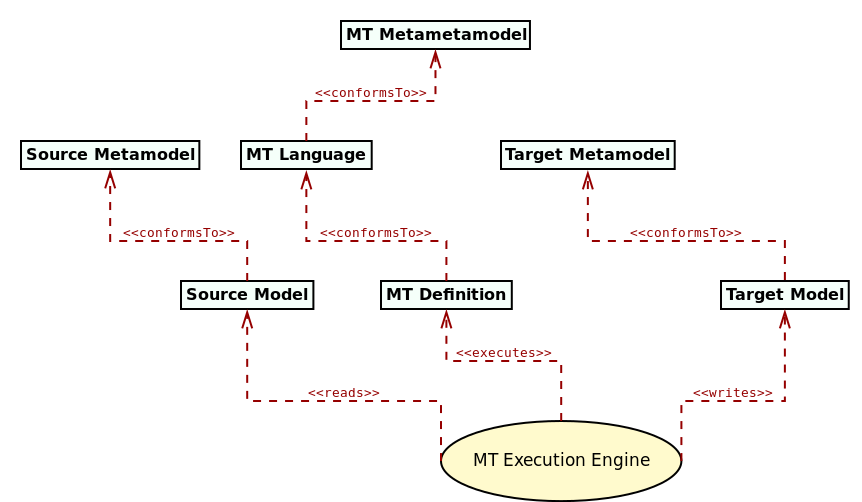
Figure 3: Basic model transformation concepts. Source: Author's drawing based on diagrams by Brambilla et al. (Brambilla, Cabot, and Wimmer 2012) (p. 18) and Czarnecki and Helsen (Czarnecki and Helsen 2006).
The literature has long considered MT themselves as models (Bézivin 2005b), thus formalisable by a metamodel and giving rise to the notion of MT languages; that is, modeling languages whose domain is model transformations. MT languages are an important pillar of the MDE vision because they enable the automated translation of models at different levels of abstraction. Figure 3 provides an example of how MT languages work, when transforming one type of model to another. However, these are not the only type of MT found in the literature.
Taxonomy
The taxonomy of MT has been investigated in great detail in the literature, particularly by Mens and Van Gorp (Mens and Van Gorp 2006) as well as by Czarnecki and Helsen (Czarnecki and Helsen 2006). For the purposes of our dissertation we are primarily concerned with what Czarnecki and Helsen identified as the top-level categories of MT: Model-to-Model (M2M) and Model-to-Text (M2T). These they describe as follows:
The distinction between the two categories is that, while a model-to-model transformation creates its target as an instance of the target metamodel, the target of a model-to-text transformation is just strings. […] Model-to-text approaches are useful for generating both code and non-code artifacts such as documents.
For completeness, there are also Text-to-Text (T2T) transforms, which merely convert one textual representation into another. Transforms of these three types are typically orchestrated into graphs — often called transform chains or MT chains8 — with M2T typically being the ultimate destination. These relationships are illustrated in Figure 4, which portraits MT in the wider MDE domain, including models and metamodels.
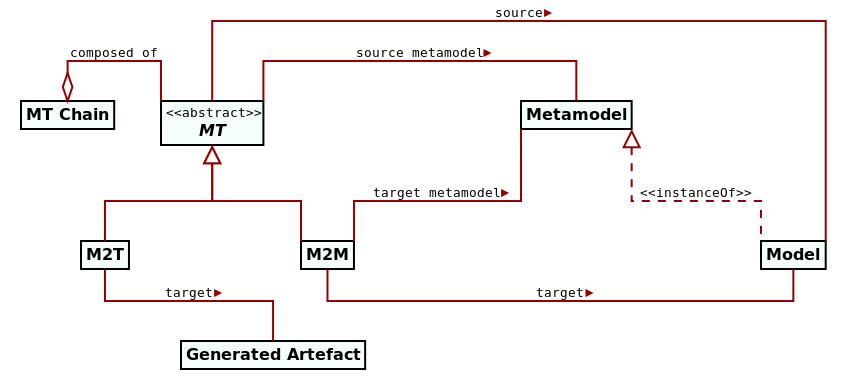
Figure 4: Relationships between MT, metamodels and models. Source: Author's drawing based on Stahl et al.'s diagram (Völter et al. 2013) (p. 60).
The importance of MT in MDE stems largely from their broad range of applications — as discussed in the next section.
Applications
The use of MT within MDE is pervasive, as demonstrated by Czarnecki and Helsen's non-exhaustive list of intended applications (Czarnecki and Helsen 2006):
- Synchronisation: The mapping and synchronisation of models, either at the same level of abstraction or at different levels, to ensure that updates are correctly propagated;
- Querying: Using queries to generate views over a system;
- Evolution: Tasks related to the evolution and management of models such as refactoring, and metamodel updating;
- Reverse-Engineering: The generation of high-level models from either source code or lower-level models.
- Code Generation: The refinement of high-level models into lower-level models and ultimately to source code — for some, a defining characteristic of the MDE approach.9
Given this large number of applications, it is unsurprising that a correspondingly large number of MT languages have emerged over time, including QVT (Query / View/ Transformation) (Kurtev 2007), ATL (Atlas Transformation Language) (Jouault et al. 2008), Epsilon (Kolovos, Paige, and Polack 2008), Kermeta (Jézéquel, Barais, and Fleurey 2009) and many others. Whilst it is undoubtedly a positive development that many different avenues are being actively explored, there are clearly downsides to this proliferation of solutions: the onus is now on the practitioner to choose the appropriate MT language, and often a deep knowledge of both MDE and the MT languages in question is required to make an informed decision. This apparent paradox of choice, at all levels, is one of the biggest challenges faced by MDE, as evidenced by adoption research.
A related problem is that, whilst MT languages have many diverse applications, they are ultimately still computer languages and thus prone to suffer from the very same malaises already diagnosed in traditional software engineering. As their use grows, issues such as technical debt (Lano et al. 2018), refactoring and difficulties around reuse (Bruel et al. 2018) will become increasingly pressing. Indeed, these and other similar issues are not specific to MT languages, but shared by all modeling languages. It is therefore crucial to understand the purpose of modeling languages and clarify their relationship with traditional programming languages.
Modeling Languages and Their Purposes
The literature commonly distinguishes between two classes of modeling languages, according to their purpose (Brambilla, Cabot, and Wimmer 2012) (p. 13):
- General Purpose Modeling Languages (GPML): These are languages that are designed to target the modeling activity in the general case, and as such can be used to model any problem domain; the domain of these languages is the domain of modeling itself. The UML (- OMG 2017) is one such language.10
- Domain Specific Language (DSL): These are languages which are designed for a specific purpose, and thus target a well-defined problem domain. They may have broad use or be confined to a small user base such as a company or a single application. As an example, the authors report in (Craveiro 2021) on the experiences and challenges of a financial company creating their own modeling DSL.
Figure 5 captures how modeling languages relate to the terminology introduced thus far.
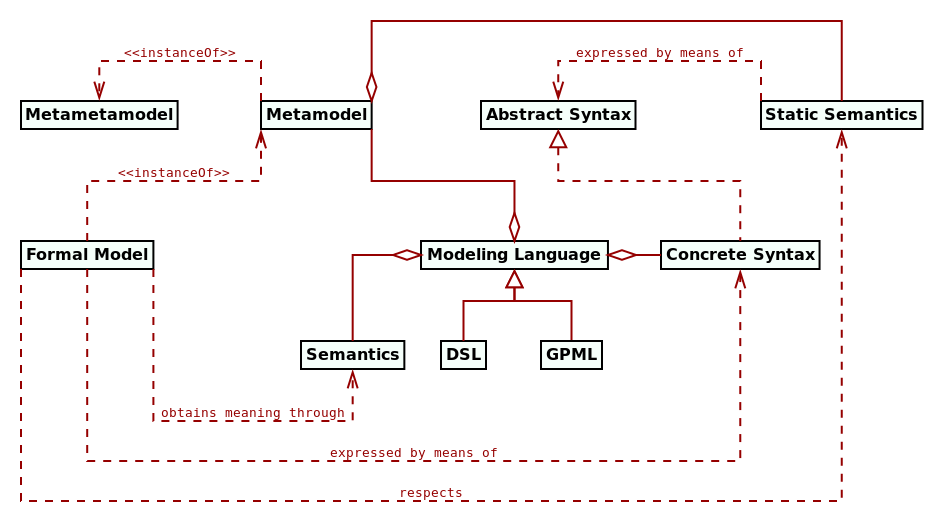
Figure 5: Fundamental MDE terminology. Source: Author's drawing based on Stahl et al.'s image (Völter et al. 2013) (p. 56)
As with most MDE terminology, this classification is not universally accepted. For instance, Stahl et al. (Völter et al. 2013) (p.58) take the view that (emphasis theirs) "[often] the term modeling language is used synonymously with DSL. We prefer the term DSL because it emphasizes that we always operate within the context of a specific domain." Somewhat unexpectedly, Jörges et al. (Jörges 2013) (p. 15) agree with this stance. We are instead of the opinion that conflating DSL with modeling languages hinders precision unnecessarily and thus is not a useful development. For the remainder of this work, we shall use the three terms (modeling language, GPML and DSL) with specifically the above meanings.11 The crux of the problem is, then, in deciding how a given modeling problem is to be tackled.
Determining the Modeling Approach
One of the first decisions faced by practitioners when when modeling a problem is the choice between using GPML or DSL. Mohagheghi and Aagedal's analysis highlights the kinds of trade-offs that must be considered (Mohagheghi and Aagedal 2007):
A metamodel’s conceptual complexity should lead to greater expressive power, and thus smaller models in size. For example, modeling languages developed for a specific domain [e.g. DSL] have more expressive power and are closer to the experts’ knowledge of the domain than general-purpose modeling languages [GPML], but may be more complex to learn for a novice.
If opting for DSL, their creation can be achieved either via extensibility mechanisms available in most GPML — such as the before-mentioned UML profiles — or by in-house language design. Regardless of the approach, the use of DSL is strongly encouraged within MDE since, as Stahl et al. tell us (p. 58), "[a] DSL serves the purpose of making the key aspects of a domain — but not all of its conceivable contents — formally expressable and modelable." (Völter et al. 2013)
A vital component of language design is choosing a notation and implementing its parsing. A simple alternative — ideal for basic requirements —is to use an existing markup language such as XML or JSON, in order to take advantage of their strong tooling ecosystem. In the XML case, an XML schema can be defined using XSD, so as to constrain XML concrete syntax. The abstract syntax will be dependent on how the XML processing is performed — i.e. using DOM, SAX or any other XML APIs. The approach is commonly referred to as XMLware (Arcaini et al. 2011), but is not without its detractors (Neubauer 2016).12
Yet another alternative, attractive for text-based notations, is to define a formal grammar for the concrete syntax (cf. Section Model Syntax) using a parser generating tool such as YACC (Johnson and others 1975) or Bison (Donnelly and Stallman 1992), and then code-generate a parser for the grammar in a general purpose programming language. The parser is responsible for processing documents written in the concrete syntax and, if valid, instantiating an abstract syntax tree: a tree representation of the abstract syntax. This approach is called grammarware in the literature (Klint, Lämmel, and Verhoef 2005) (Paige, Kolovos, and Polack 2012), and has historically been used to define programming languages, but it is equally valid for modeling textual DSL.13
Finally, the more modern take on this problem is called modelware because it relies on model-driven principles and tooling. It is implemented using tools such as XText (Eysholdt and Behrens 2010), which generate not just the parser but also customisable abstract syntax, as well as providing IDE support for the newly-designed language. Modelware is the preferred approach within the MDE community because it embodies many of the core principles described in this document, and, in addition, some modelware stacks offer integrated support for graphical notations.14
Nonetheless, regardless of the specifics of the approach, there are clear similarities between traditional programming languages and modeling languages, as we shall see next.
Modeling Languages and Programming Languages
There are obvious advantages in clarifying the relationship between programming languages and modeling languages, because the latter can benefit from the long experience of the former. Predictably, the literature has ample material on this regard. Whilst discoursing on the unification power of models, Bézivin spoke of "programs as models" (Bézivin 2005b); France and Rumpe tell us that "[source] code can be considered to be a model of how a system will behave when executed." (France and Rumpe 2007) Indeed, from all that has been stated thus far, it follows that all general purpose programming languages such as C++ and Java can rightfully be considered modeling languages too and their programs can be thought of as models implemented atop a grammarware stack.
Here we are rescued by Stahl et al., who help preserve the distinction between programming languages and modeling languages by reminding us that they have different responsibilities (emphasis ours): "The means of expression used by models is geared toward the respective domain’s problem space, thus enabling abstraction from the programming language level and allowing the corresponding compactness." (Völter et al. 2013) (p. 15) That is, programming languages are abstractions of the machine whereas modeling languages are abstractions of higher-level problem domains — a very useful and concise separation (cf. Spaces and Levels of Abstraction).15
With this, we arrive at the taxonomy proposed by Figure 6.
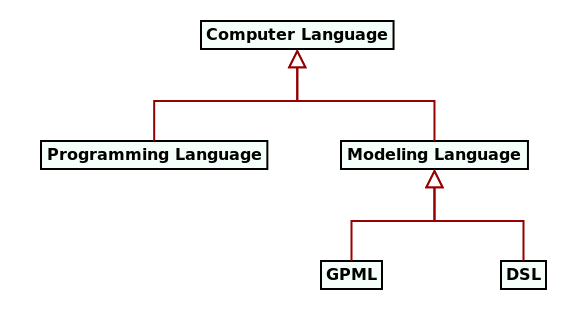
Figure 6: Taxonomy of computer languages within MDE.
A related viewpoint from which to look at the relationship between modeling languages and programming languages is on how information can be propagated between the two via MT (cf. Section Models and Their Transformations). The simplest form is via forward engineering, whereby a model in a modeling language is transformed into a programming language representation, but changes made at the programming language level are not propagated back to the modeling language.
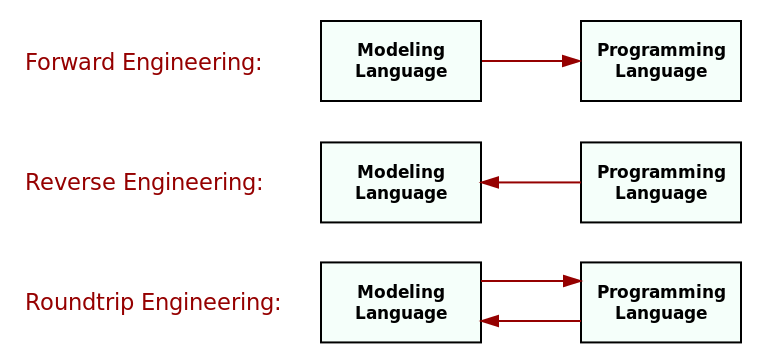
Figure 7: Propagating information between modeling languages and programming languages. Source: Author's drawing based on an image from Stahl et al. (Völter et al. 2013) (p. 74).
The converse happens when using reverse engineering: a model in a modeling language is generated by analysing and transforming source code in a programming language. Clearly, there are difficulties in any such an endeavour due to the mismatch in abstraction levels, as explained above. Finally, the most difficult of all scenarios is RTE (Round Trip Engineering), in which both modeling and programming language representations are continually kept synchronised, and changes are possible in either direction. Figure 7 illustrates these three concepts.
As briefly alluded to in Section Models and Their Transformations, these and other related topics fall under the umbrella of model synchronisation within MDE literature. They are addressed in From Problem Space to Solution Space, which starts to delve in more detail into MDE's aspirations of matching modeling languages to different abstraction levels.
Bibliography
Footnotes:
The quote was sourced from Podnieks (Podnieks 2017) (p. 19). As we could not locate an English translation of "General Model Theory" (Stachowiak 1973), we were forced to rely on secondary sources, including Podnieks, to access fragments of Stachowiak's work. Podnieks' paper is of great interest with regards to the philosophical aspects of modeling, but lays beyond the scope of our dissertation.
The paper is recommended reading to anyone with interest in the philosophical aspects of modeling and its relation to computer science. Readers are also directed to Czarenecki (Czarnecki et al. 2000), Chapter 2 "Conceptual Modeling" and to Bézivin (Bézivin 2005b), Section 3.1. "On the meaning of models". Incidentally, it was Bézivin's paper that guided us towards Rothenberg's work.
An idea which is, in itself, a model taken from software design (Al-Fedaghi 2016).
It is worth noticing that the use of metamodels in the context of OO languages has a long history in computer science. Henderson-Sellers et al. (Henderson-Sellers et al. 2013), in their interesting and thought provoking work, report of their emergence within this context: "The use of metamodels for OO modelling languages was first promoted in 1994 […] and consequently realized in Henderson-Sellers and Bulthuis (Henderson-Sellers and Bulthuis 2012) in their creation of metamodels for 14 out of a list of 22 identified (then extant) modelling languages (at that time often mis-called methodologies)." These retro-fitting steps were key to the modern understanding of the role of metamodels in modeling languages.
Seidewitz calls this a reflexive metametamodel (Seidewitz 2003) whereas Álvarez et al. (Álvarez, Evans, and Sammut 2001) favour the term meta-circular, but both are used with equivalent meaning.
Jörges et al. refer to these meta-layers as metalevels (Jörges 2013) (p. 17).
The historical context in which the four-layer metamodeling hierarchy emerged is quite interesting and illuminating with regards to its spirit. Henderson-Sellers et al. (Henderson-Sellers et al. 2013) chronicle it quite vividly: "Around 1997, the OMG first publicized their strict metamodelling hierarchy […] apparently based on theoretical suggestions of Colin Atkinson, not published until a little later […]. The need for a multiple level hierarchy […], thus extending the two level type-instance model, was seen as necessary in order to 1) provide a clear means by which elements in the (then emergent) modelling language of UML could be themselves defined i.e an M3 level and 2) acknowledge the existence at the M0 level of individual (instances) of the classes designed at the M1 level — although for the OMG/UML world these were seen as less important because such instances only exist as 'data' within the computer program and, in general, do not appear within the modelling process."
Wagelaar's analysis of particular interest in this regard: "Composition of model transformations allows for the creation of smaller, maintainable and reusable model transformation definitions that can scale up to a larger model transformation." (Wagelaar 2008)
In Jörges words (Jörges 2013) (p. 19): "Code generation is thus an enabling factor for allowing real model-driven software development which treats models as primary development artifacts, as opposed to the approach termed model-based software development […]."
A simplification; technically, UML is a modeling language suite rather than a modeling language because it is comprised of a number of modeling languages designed to be used together. Note also that not all UML models are formal models but UML models can be made formal through the use of UML Profiles and a formal definition of static semantics.
In Stahl et al.'s defence, most GPML require a degree of extensibility in order to support formal models — e.g., in the case of UML, the creation of profiles are typically required, and thus considered a DSL. In this sense, plain GPML appear to be of a limited use in a MDE context. Nonetheless, our point is that, even without further customisation, GPML provide a sufficient basis for simpler automation use cases. Therefore, in our opinion, it is incorrect to think of GPML as "merely" tools for some form of Model-Based Engineering (MBE).
An XMLWare-based stack was the solution used by a financial company, whose experiences are narrated in (Craveiro 2021).
Several programming languages also offer modern parser libraries, such as C++'s Boost Spirit (Boost 2018) or Java's ANTLR (Parr 2013). These are more appealing to typical software developers (as opposed to compiler writers) because they provide a better fit to their workflows.
Seehusen and Stølen 's evaluation report of GMF (Graphical Modeling Framework) serves as a typical example (Seehusen and Stølen 2011). GMF is part of the vast EMF (Eclipse Modeling Framework) modelware stack; those specifically interested in EMF are directed instead to Steinberg et al. (Steinberg et al. 2009).
These camps are not quite as distinct as they may appear, and many are working to shorten the differences. On one hand, there are those like Madsen and Møller-Pedersen who propose a more direct integration of modeling concepts with programming languages themselves (Madsen and Møller-Pedersen 2010). On the other hand, there are also those like Badreddin and Lethbridge, proponents of MOP (Model Oriented Programming), who defend making modeling languages more like programming languages (Badreddin and Lethbridge 2013). Both approaches show a great deal of promise but, given their limited application at present, we declined to investigate them further.